Ciągi - blagam o rozwizanie zadania Robert:

	(n + 1)! * (2n)!
Dany jest ciąg o wyrazie ogólnym an =		, n ∊ N
	(2n + 1)! * n!

dodatnich a) zbadaj monotoniczność tego ciągu

	11
b) sprawdź ile wyrazów tego ciągu jest większych od
	21

powodzenia:): a) najpierw sprawdź czy to ciąg ary albo geo, jeśli ary, to rosnący jest wtedy gdy r>0, jesli geo to q>0, jeśli stały to r=0 lub q=0, malejący r<0 lub q<0 potem sprawdż dla wyrazów a_n−1 i dla a_n

	11
b) podstaw		i rozwiąż nierówność
	22

Bogdan: Już wczoraj przekazałem wskazówkę, nie czytasz swoich wpisów? Jest tu: 26363

Bogdan: Nie ma potrzeby sprawdzać, jaki to jest ciąg: arytmetyczny, czy geometryczny, czy inny.

ula: dla (n+1) − podstaw to zamiast n

(n+1+1)!*[2(n+1)]!		(n+2)!*(2n+2)!		n+2
	=		=
[2(n+1)+1]*(n+1)!		(2n+3)!*(n+1)!		2n+3

monotoniczność badamy odejmująz a(n+1)−a(n) jeśli wyjdzie >0 to ciąg jest rosnący jeśli wyjdzie <0 to jest malejący

	n+1
a(n) po skróceniu silni wynosi		− odejmij
	2n+1

ula: wyklorzystaj to zadanie wcześniejsze tam obliczyłam a(n) po skróceniu silni

n+1
	>1121
2n+1

21n−21−11(2n+1)
	>0
21(2n+1)

mianownik jest zawsze większy od zera bo n(liczba wyrazów)jest zawsze>0 więc 21n+21−22n−11>0 n<10 Odp. 9 wyrazów

Edytka: Po skróceniu silni to znaczy jak? (2n)! i (n)! jak to skrócić?

sushi_ gg6397228: mozna skrocic (2n)! i (2n+1)!

Edytka: A dlaczego tak można skrócić?

sushi_ gg6397228: (2n+1)!= (2n)! * (2n+1) i teraz mozna zredukowac

Edytka: A dlaczego tak? jakiś wzór czy co?

Edytka: Dlaczego zostało n+1/2n+1? Przecież jak się skróci to jeszcze zostaję n! Prawda? Czy nie?

sushi_ gg6397228: to sie skrocilo z czym innym; zapisz o ktory moment sie Tobie rozchodzi

sushi_ gg6397228:

	(n + 1)! * (2n)!
an =
	(2n + 1)! * n!

skracanie czerwone z czerwonym, zielone z zielonym−−> zostaje to co mialo byc

Julka:

	−1
Ej dobra, pytanie. Różnica wyszła mi		Obliczyłam delte, wyszły dwa
	4n2+8n+3

pierwiastki ujemne. I to tu mam napisać, że te pierwiastki są<0 i ciąg jest malejący?

Mateusz: Tyle czasu to liczyłaś a po co tu Δ liczyc bez liczenia delty mozna okreslic jakie to wyrazenie jest tzn czy jest mniejsze lub większe od 0 trzeba tylko sie dobrze przyjrzeć

Julka: Nie no ja to zadanie dopiero dzisiaj zaczęłąm rozwiązywać, nie mogłam rozkminić końca sama więc szukam pomocy Hm..skoro mówisz, że można to się przyjrze..

Mateusz:

	a
aa podpowiem np		>0 <=> a>0 i b>0 lub a<0 i b<0 teraz ty rozpatrz dla drugiego
	b

przypadku i sprawdz co pasuje i okres czy ciąg w sumie jest malejący czy rosnący

Julka: o jezu, n∊N+

Julka: nawet nie trzeba się bawić w to co napisaleś ale dzięki!

Dres: Odświeżam. Mnie wychodzi w tym zadaniu jakiś chłam, bo według moich wyliczeń funkcja jest malejąca dla naturalnych dodatnich. Podpunkt b daje radę, ale a za cholerę

Mila: I sposób:

	(n+1)*n!*(2n)!		n+1
an=		=
	(2n)!*(2n+1)*n!		2n+1

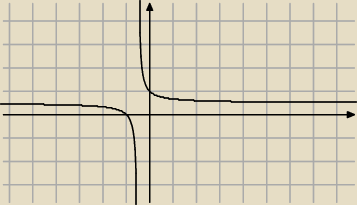
I to mógłby być , koniec, ponieważ punkty wykresu ciągu należą do wykresu funkcji homograficznej

	x+1
f(x)=		a to jest funkcja malejąca dla x>0, zatem dla n∊N+, ciąg malejący.
	2x+1

II sposób:

	n+1+1		n+2
an+1=		=
	2(n+1)+1		2n+3

badamy znak różnicy:

	n+2		2n+1		(n+2)(2n+1)−(n+1)(2n+3)
an+1−an=		−		=		=
	2n+3		n+1		(2n+3)(2n+1)

	2n2+n+4n+2−2n2−3n−2n−3		−1
=		=		<0 ⇔ciąg malejący.
	(2n+3)(2n+1)		(2n+3)(2n+1)

Dres: Miałem zastrzeżenia co do sposobu drugiego właśnie, bo wszystko doprowadziłem do takiej samej postaci jak Ty, ale w końcu dla ujemnego licznika przy rosnącym mianowniku wyrażenie to będzie rosnące w całej dziedzinie... Pierwszy sposób wygląda za to idealnie, nie pomyślałem że mogę narysować wykres funkcji homograficznej! Peace

Dres: Edit! Zapomniałem napisać z rozpędu jednej rzeczy, sorry za spam. Wynika z tego, że jeśli przy badaniu znaku różnicy otrzymamy wynik mniejszy od zera, to funkcja jest malejąca, jeśli równy zero jest stała, a jeśli większy od zera rosnąca?

Mila: